|
|
|
$$2p = L \times 5$$
Perímetro
$$L = \frac{2p}{5}$$
$$A = \frac{2p \times a}{2}$$
Área
$$a = \frac{2A}{2p}$$
Apotema
$$2p = \frac{2A}{a}$$
Perímetro
$$d = \frac{L (\sqrt{5} + 1)}{2}$$
Diagonal
$$L = \frac{d (\sqrt{5} - 1)}{2}$$
Lado
Número fijo
$$f = 0,688 = \frac{a}{L}$$
Número fijo
$$a = L \times f$$
Apotema
$$L = \frac{a}{f}$$
Lado
Constante de área
$$\varphi = 1,720 = \frac{A}{{L}^2}$$
Constante de área
$$A = {L}^2 \times \varphi$$
Área
$$L = \sqrt{\frac{A}{\varphi}}$$
Lado
Pentágono escribiendo
$$L = \frac{ R\sqrt{10 - 2 \sqrt{5}} }{2}$$
Lado
$$a = \frac{ R \times \left( \sqrt{5} + 1 \right) }{2}$$
Apotema
$$A = \frac{ {R}^2 \times 5 \sqrt{ 10 + 2 \sqrt{5} } }{8}$$
Área
$$R = d \left[ \sqrt{ \frac{5 - \sqrt{5}}{10} } \right]$$
Radio C. circunscrita
$$d = R \left[ \sqrt{ \frac{5 + \sqrt{5}}{2} } \right]$$
Diagonal
Definición
Un pentágono es un polígono de cinco lados. Un pentágono regular es un polígono regular con cinco lados y cinco ángulos congruentes.
Propiedad
- Polígono de cinco lados
- El pentágono regular tiene cinco lados y cinco ángulos congruentes, 108° de ancho
- Un pentágono regular se puede inscribir o circunscribir a una circunferencia
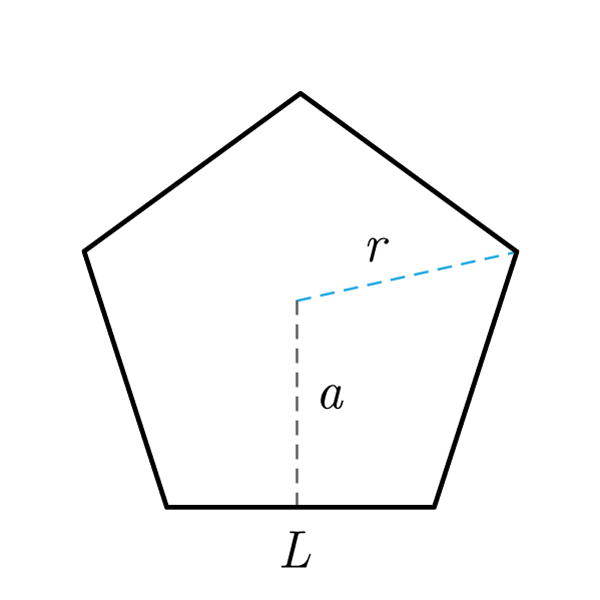
Fórmulas Pentágono
| Dado | Fórmula |
|---|---|
| Perímetro | 2p = L × 5 |
| Área | A = (2p × a) / 2 |
| Diagonal | d = [L(√5 + 1)] / 2 |
| Lado | L = 2p / 5 |
| Número fijo | f = 0,688 = a / L |
| Constante de área | φ = 1,720 = A / (L2) |
| Apotema | a = (2A) / (2p) |
| Perímetro | 2p = (2A) / (a) |
| Lado | L = [d(√5 - 1)] / 2 |
| Apotema | a = L × f |
| Lado | L = a / f |
| Área | A = L2 × φ |
| Lado | L = √(A / φ) |